Expanding Major Interval Music Theory to Minors
The names of intervals are stated in such terms as a second, third, fourth, fifth, and continue up to fifteenths as was stated in the Music Theory of Intervals.
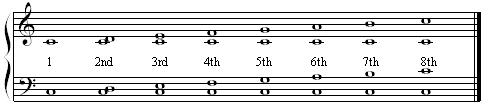
Take a quick review of the Major Intervals
Making the Interval Minor
The 2nd, 3rd, 5th, 6th, and 7th can all be made minors by stepping down a half step.
Therefore you can get a minor 2nd, a minor 3rd, and a minor 6th.
However, the 5th when made flat is typically called a tritone or a flat 5, and not very often referred to as a minor 5th, but more often as a diminished 5th.
The 7th when made flat is called a dominate 7th, which will be come more clear when we study chord structure. It is sometimes referred to as a minor 7th.
Notice that we didn’t call the 4th a minor. On the scale structure when a fourth is made flat it is a major 3rd. Some will argue that it is possible to have a minor 4th.
Technically, it might be applied when you have a minor 3rd and a minor 4th. Since this is a bit obscure at this point just stick with the the others.
Most often in relating to the 4th we migh augment it or raise it a half step. It would be a sharp 4 (#4). And that is the same note as the flat 5.

Working with the Minor Intervals
If we take our major intervals and flat or raise them as discussed above the new ones become the m2nd, m3rd, +4th, dim5th, m6th, and a dom7th.
The following measure shows the minor intervals for the C octave.

Here are the rules for finding minor intervals.
| Interval | Example | Label |
| Minor Second (1 half step) |
C to Db | m2 |
| Minor Third (3 half steps) |
C to Eb | m3 |
| Augmented Fourth (6 half steps) |
C to F# | +4 |
| Diminished Fifth (6 half steps) |
C to Gb | dim5 |
| Minor Sixth (8 half steps) |
C to Ab | m6 |
| (dominant) Seventh* (10 half steps) |
C to Bb | 7 |
*The dominate Seventh is shown as just 7 referred to as minor 7 and dominate 7th.

